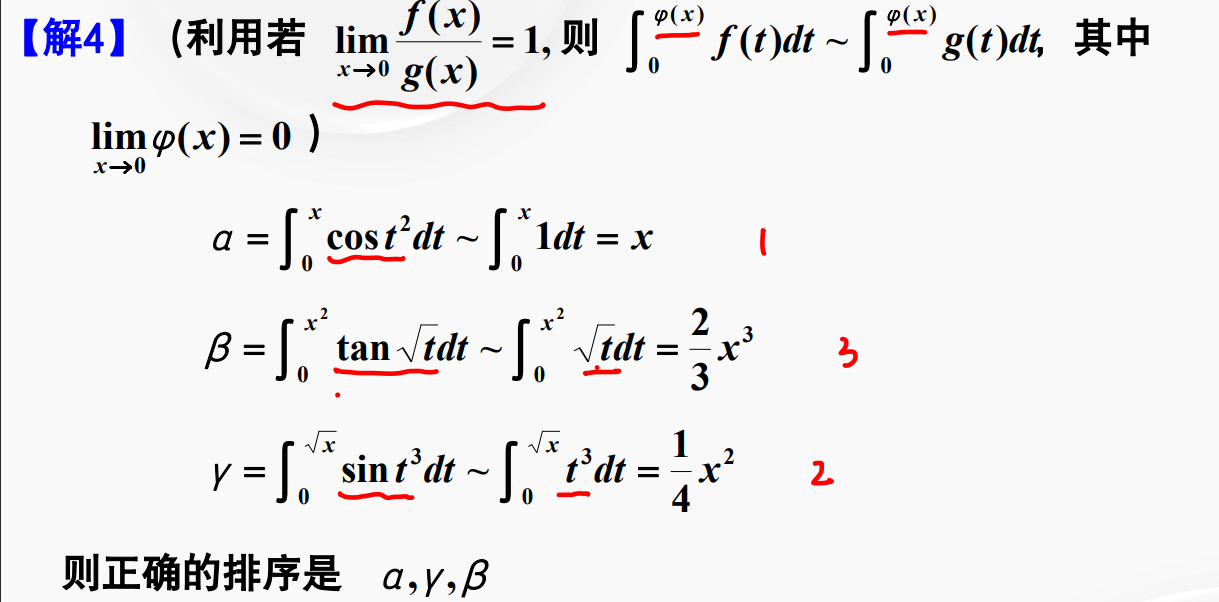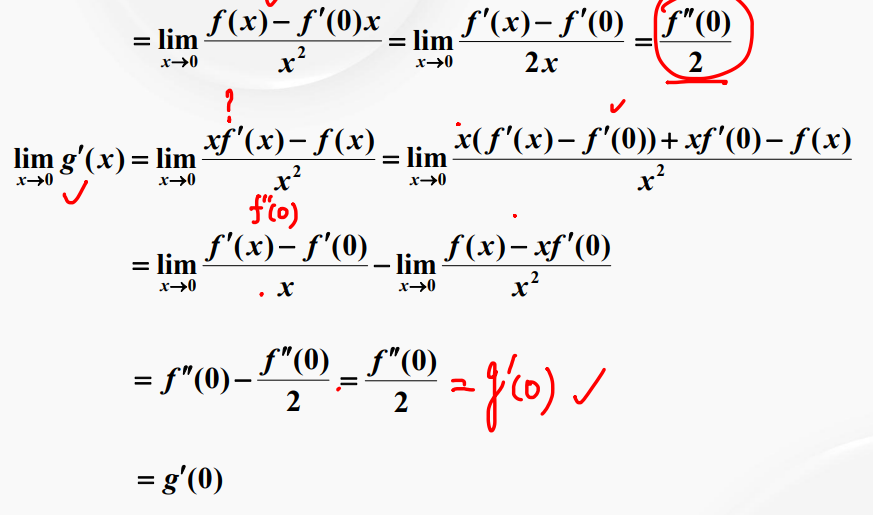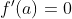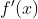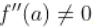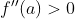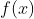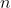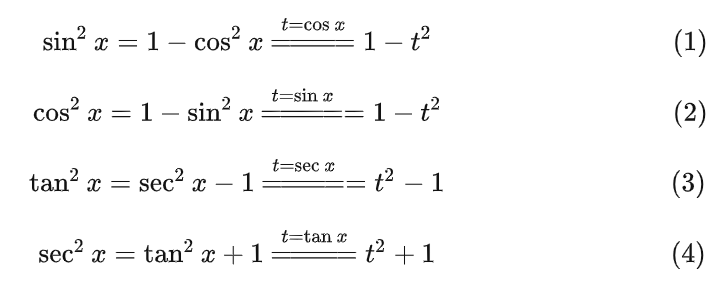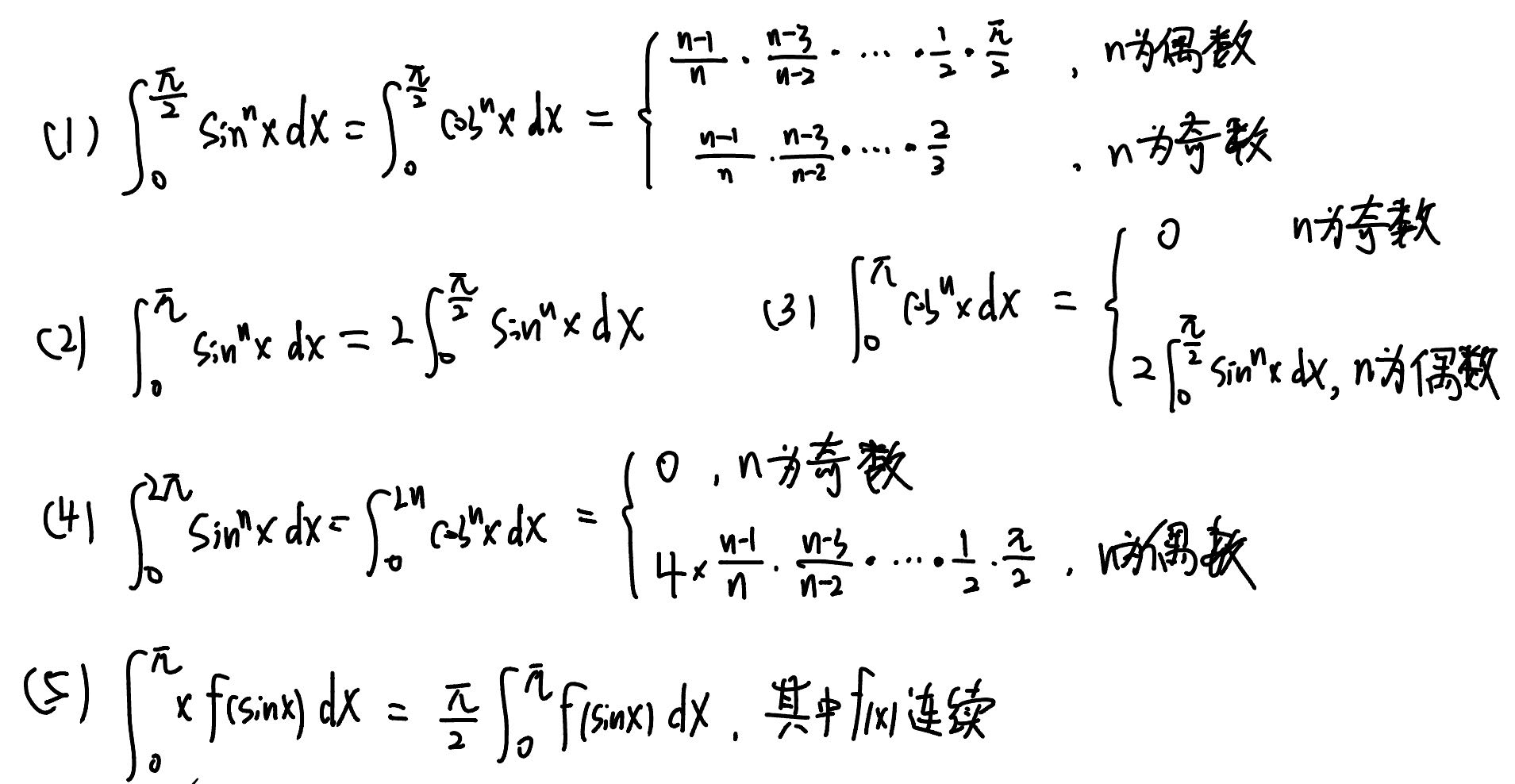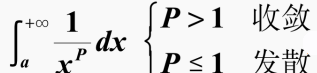函数周期性
周期函数的原函数是周期函数的充要条件是其在一个周期上的积分为0.
高等数学辅导讲义P5
函数有界性
f(x)的导数在区间I(有限)上有界 => f(x)在I上有界
高等数学辅导讲义P5,用拉格朗日中值定理证明
保号性
无穷小比较
夹逼定理和定积分的精确定义区别
变化部分是主体部分的次量级用夹逼
变化部分是主体部分的同量级用定积分定义
递推数列(小南)
递推数列求极限
法一:先证数列收敛(单调有界准则)再求极限
法二:先求出极限,再证极限为A
设数列{xn}由x1=a,xn+1=f(xn)(n=1,2,…),xn∈I所确定,
①若f(x)在I上单调递增,则当x1≤x2时,{xn}单调增; 当x1≥x2时,{xn}单调减;
②若f(x)在I上单调减,则{xn}不单调,选用法二
确定极限式中的参数
### 无穷小阶比较
洛必达、等价无穷小代换、泰勒
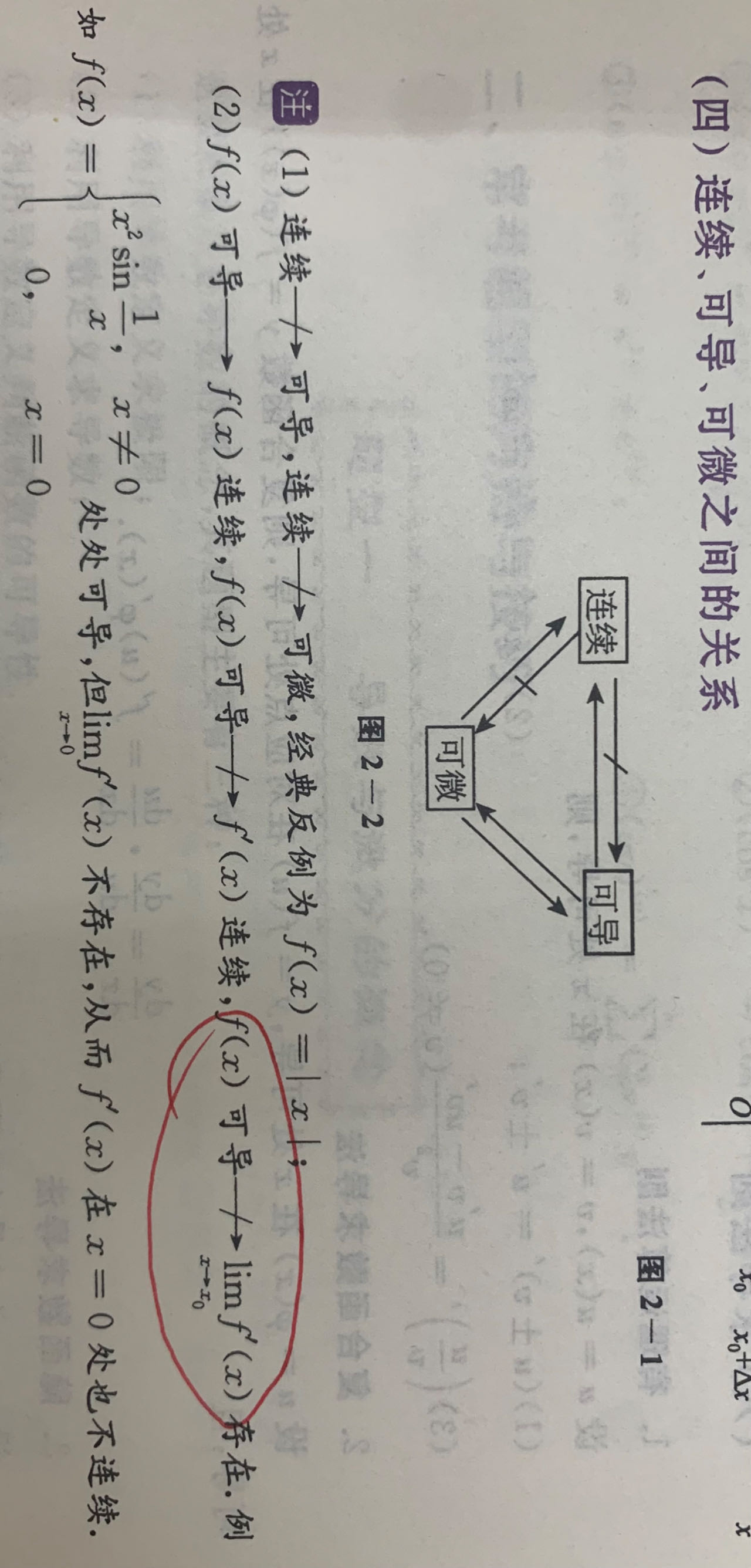
连续性间断点
导数与微分
洛必达使用条件
| 条件 | 使用洛必达法则最多可用到 |
|---|---|
| 1)f (x)n 阶可导 | f(n-1)阶导数 |
| 2)f (x)n 阶连续可导 | f(n)阶导数 |
反函数求导
注意最后反函数带进去的变量是y,要先利用x反求出变量y的值
导数定义求极限
导数定义判断可导性
拐点和极值点的判定
拐点为极值点再升一阶,注意:第三充分条件变成奇数为拐点
有关绝对值的一些结论*
罗尔定理推论
若再区间 I 上f(n)(x) ≠ 0, 则方程 f(x)=0 在 I 上最多有n个实根.
可用反证法证明,假设不止n个.
微分中值定理有关证明题(难死了)
辅助函数归纳
记住画蓝色圈的第四个就好了
证明一个点—-单中值问题
证明存在两个中值—–双中值问题
-
不要求两个中值不相等
-
用两次中值定理,一次拉格朗日,一次柯西
-
-
要求两个中值不相等
-
将区间[a,b]分为两个子区间,在两个子区间上分别用拉格朗日中值定理(一般题目第一问的点就是划分点,没有的话可以直接先用中值定理来找划分点)
-
证明存在一个中值使高阶导数≥0(n≥2)
-
用带拉格朗日余项的泰勒公式,其中x0点选取题目中提供函数值和导数值信息多的点.
泰勒在x点处展开带值(骚操作)
上下两个式子中x不是一个意思,下面的写成t更好理解,上面是在0处展开,下面的式子把x写成t,就是f(x)在参数t处展开当x=0时的值。
泰勒公式中存在x、x0两组变量(介值属于类似一个二元函数) ,固定任意一组另一组变化等式皆成立。表示f(x)的n阶导数,等号后的多项式称为函数f(x)在x0处的泰勒展开式,剩余的Rn(x)是泰勒公式的余项,是(x-x0)n的高阶无穷小。
一元函数积分
原函数存在性
-
若f(x)在区间I上连续,则f(x)在区间I上必有原函数
-
若f(x)在区间I上有第一类间断点,则f(x)在区间I上没有原函数
积分公式表
积分常用方法
(1)一般法(部分分式法);
(2)特殊方法(加项减项拆或凑微分绛幂);(经常用加项减项拆)
2)倒代换(即令 x = 1/t):设m,n 分别为被积函数的分子、分母关于x 的最高次数,当 n-m>1时,用倒代换可望成功;
三角有理式的积分常用方法
ln后记得加绝对值
万能代换
令tan(x/2)=t , sinx=2t/(1+t2) , cosx=(1-t2)/(1+t2) , dx=2/(1+t2)dt
换元
i)若 R(- sin x,cos x) = -R(sin x,co s x ) , 则 令u=cosx;
ii)若 R(sin x,- cos x) = -R(sin x,cos x ) , 则 令u=sinx;
iii)若 R(- sin x,- cos x) = R(sin x,cos x ) , 则 令u=tanx.
常用的三角代换
定积分的存在性
1)必要条件 f ( x) 有界;(可积必有界)
2)充分条件
-
f ( x) 在[a,b]上连续,则定积分存在;
-
f ( x) 在[a,b]上有界且只有有限个间断点,则定积分存在;
-
f ( x) 在[a,b]上仅有有限个第一类间断点,则定积分存在;
定积分计算公式
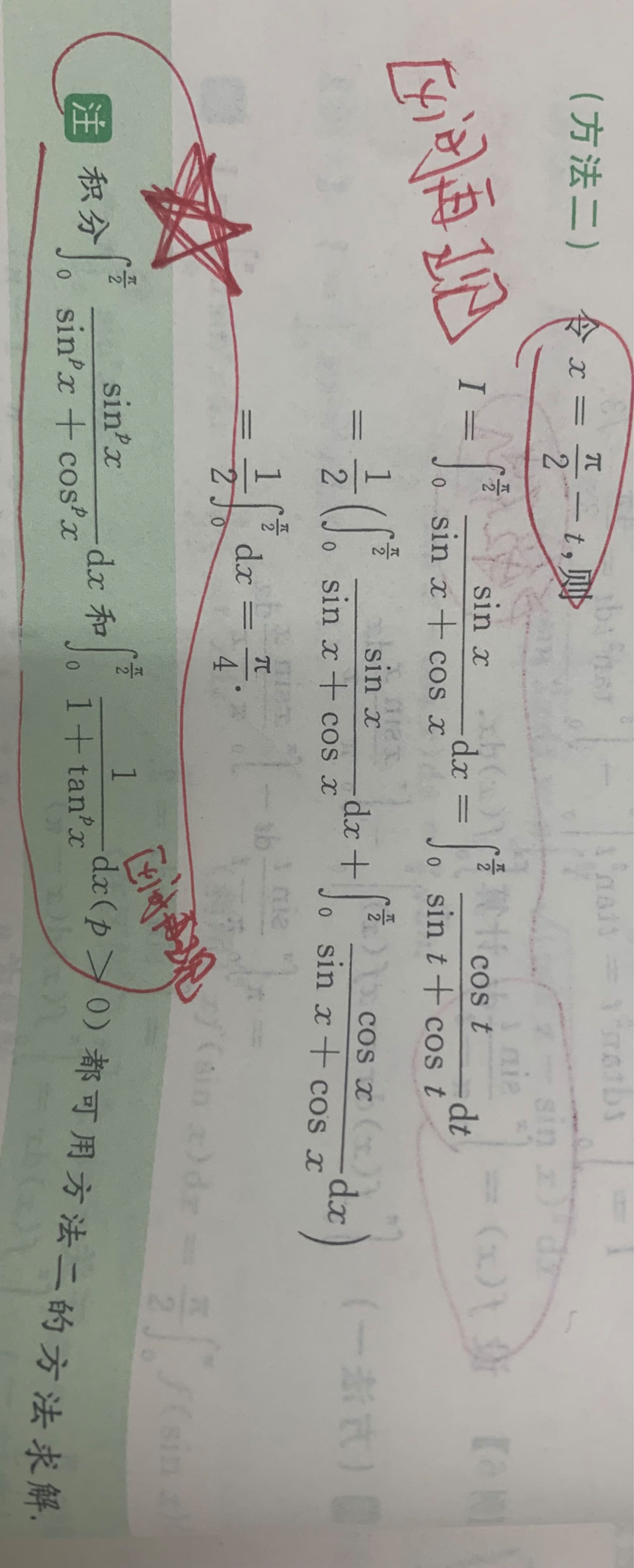
区间再现
令x=a+b-t 或者 换元使得积分区间相同,有时候在积分区间0到无穷做倒代换也相当于区间再现
变上限积分的连续性可导性
积分不等式
sinx<x<tanx
x/(1+x)<ln(1+x)<x
柯西积分不等式:
比较积分大小:出的题目都是一个被积函数恒大于另一个,只需要带特殊值进去算就行。
题目提供了单调区间,然后证明积分不等式,一般用变上限积分
出现f(x)与f(x),,联系函数和其导数可用,拉格朗日中值定理,或者将fx写为导数的积分
反常积分
p积分在无穷区间
p积分在无界函数
赞赏 微信赞赏
微信赞赏 支付宝赞赏
支付宝赞赏